Xander Home Study Guide: K to 12 Grade 8 MATH

FIRST QUARTER

I. Patterns and Algebra

Patterns:

When you look around you, you can see patterns everywhere like the constellations that you see in the night sky or patterns painted around your school.Patterns are everywhere and they are important because we look and solve things in an organized way but did you know that numbers have patterns too? Their patterns can be found when you understand the concept of polynomials and the methods used to solve them.

Using patterns to simplify mathematical expressions has advantage
depending on what the expressions have. These expressions are an example of a mathematical expressions solved by using patterns:

97 × 103 = 9991

25^2 ;25 × 25 = 625

99^2 * 99;99^3;99 x 99 × 99 = 970299

Each of the expressions have their own patterns in them. Solving them maybe hard if you don't use patterns but if you use the patterns you can see that the exponents breaks up into a multiplication pattern. Without using any patterns, you will encounter difficulties and misunderstandings.

The patterns you encountered above are examples of the many situations where we can apply the knowledge of Special Products. Varied activities will be given to help you solve unknown quantities in geometric problems. The I.R.F worksheet will determine that will determine your knowledge about the topical question.

Cross Number puzzle:

Across:

(a + 3) + (a + 3)

a^2 +6a +9

(b + 4a)^2

-81 + 6b

2a(-8a + 3a)

b^2 +6a

(b-4)(b-4)

-16a^2 + 2ab

-2a(b+3–2a)

4a^2 - 2ab - 6a

(5b^2+7a^2)(-5b^2+7a^2)

49a^4 - 25b^4

(a - 6b)(a + 6b)

a^2 - 36b^2

Down:

(a + 9)(a - 9)

a^2 - 81

(3+a+b)^2

a^2 + 2ab + 6a + b^2 + 6b + 9

(3b–4a)(3b–4a)

9b^2 - 12ab + 16a

(-4a + b)(4a + b)

+b^2

06.10.15

- The given expressions have numerical patterns to help you answer the expressions mostly multiplication patterns. They may have some difficulties in answering them but once you find the pattern, it will lessen the difficulty and you can use the appropriate technique to solve them accurately. The techniques used above are numerical[Multiplication],monomial square, and monomial cube methods to solve the expressions.

Excercise 3

see:Answer Key for Cross number puzzle (above) and Exercise 3

This activity will enable you to review multiplication of polynomials.

Case I.

(x+5)(x-5)

x^2 - 5x + 5x - 5^2

x^2 - 25

(a-b)(a+b)

a^2 + ab - ab - b^2

a^2 - b^2

(x+y)(x-y)

x^2 - xy + xy - y^2

x^2 + xy - y^2

(x-8)(x+8)

x^2 + 8x - 8x - 8^2

x^2 - 64

(2x+5) (2x-5)

4x^2 - 10x + 10x - 5^2

4x^2 - 25

Case II.

(x+5)^2

x^2 + 2(5x) + 5^2

x^2 + 10x + 25

(a-b)^2

a^2 - 2(ab) - b^2

a^2 - ab - b^2

(x+y)^2

x^2 - 2(xy) - y^2

x^2 - xy - y^2

(x-8)^2

x^2 - 2(8x) - 8^2

x^2 - 16x - 64

(2x+5)^2

4x^2 + 2[2x(5)] + 5^2

4x^2 - 20x + 25

Case III.

(x + 5)^3

x^3 + 15x^2 + 75x + 125

(a–b)^3

a^3 – 3a^2 b+ 3ab^2 – b^3

(x+y)^3

x^3 + 3x^2 y + 3xy^2 + y^3

(x+4)^3

x^3 + 3x^2y 12x^2y + 48x + 64

Case IV.

(x+2y)^2

a^2 + b^2 + c^2 + 2ab + 2ac + 2bc

(a+b+c)^2

x^2 + y^2 + z^2 + 2xy + 2xz + 2yz

(m + 2n – 3f)^2

m^2 + 4n^2 + 9f^2 + 4mn – 6fm – 12fn

The goal in this section is to learn and understand key concepts related

to finding special products. There are special forms of algebraic
expressions whose products are readily seen. These are called
special products. There are certain conditions which would make a
polynomial special. Discovering these conditions will help you find the product of algebraic expressions easily.

06/17/15

Squaring a Binomial

In squaring a Binomial you have to express it as (x+y)^2 or (x+y)(x+y).

Activity 4: Fold to square

Description: This activity is used to help you understand binomial squaring through the method of paper folding. You can also investigate the patterns you find for each fold.

Materials: An 8x8 paper

Procedure:

Fold your paper from an edge to make a crease.
Fold it again from the upper right edge to make another crease.
Continue the activity to another paper but make it in folds of two inches. Then do the same in another on folds of three inches.
After that you should be able to see the patterns below:

You can see that you have formed 4 regions in each paper, each region has a shape of a square.There are at least 8 dimensions on each square.
The area of each region has a pattern of (x+1).
The sum of the areas are 49x^2 + 14x + 1y^2 + 2y.
If you replace 1 by 'y' the sum would possibly become 1y.

These patterns are used to emphasize the paper folding patterns

(x+1)^2

First Term: x^2
Second Term:2x
Third Term: 1
Total Term: x^2 + 2x + 1

(x+2)^2

First Term: x^2
Second Term:4x
Third Term: 4

(x+3)^2

First Term: x^2
Second Term:6x
Third Term: 9

(x+y)^2

First Term: x^2
Second Term:2xy
Third Term: y^2

The pattern you can find above is the fast pattern in solving the square of a binomial.

The first term in the product is squared unlike the first given term.
The last term in the product is also squared unlike the last given term.

Observe the following examples:

(x – 3)^2 = (x)^2 – 3x – 3x + (3)^2
(x + 5)^2 = (x)^2 + 5x + 5x + (5)^2

Let's Practice!

Square the following binomials using the pattern you have learned.

(s + 4)^2 = s^2 + 8s + 16
(w– 5)^2 = w^2 – 10w + 25
(e – 7)^2 = e^2 – 14e + 49
(2q – 4)^2 = 4q^2 – 16q + 16
(3z + 2k)^2 = 9z^2 + 12zk + 4k^2
(5d – 7d^2^t)^2 = 25d^2 – 70d^3^t + 49d^4t^2
(7q^2 * w^2 – 4w^2)^2 = 49q4w4 – 56q2 w4 + 16w4
(2/3e – 6)^2 = 49e^2 – 8e + 36
(45kj – 6)^2 = 16/25k^2j^2 – 48/5kj + 36
[(x + 3) – 5]^2 = x^2 – 7x + 64

Binomial Squares are one of the many patterns in special products. But there are still many patterns you can solve.

06.24.15

For any real number (x+y+z)^2

(x+y+z)(x+y+z)

x^2 + y^2 + z^2 + 2(x)(y) + 2(x)(z) + 2(y)(z)

x^2 + y^2 + z^2 + 2xy + 2xz + 2yz

Example:

(2x + 8y + 12)^2

2x^2 + 8y^2 + 12^2 + 2(2x)(8y)+ 2(2x)(12) + 2(8y)(12)

4x^2 + 32y^2 + 144 + 32xy + 48xy + 192y

Activity 5: Discover me After!

Objective: Through paper folding and cutting, you will discover a pattern that will help you understand how trinomials are squared.
Directions:

Get a 10x10 square paper.
Mark the vertical side with numbers (Example 7,3,1).
Mark the horizontal side with letters (Example a,b,c).
Fold the numbered side vertically and make a crease.
Do the same thing on the horizontal side.

Descriptions:

As you can see, there are 9 regions formed with a 3x3 dimension. If you represent a region with a letter without replacing the number, you will see that you can represent (7a + 3b + a).

Observe the following:

(x+y+z)^2 = x^2 + y^2 + z^2 + 2xy + 2xz + 2yz
(x+y-z)^2 = x^2 + y^2 + z^2 + 2xy - 2xz - 2yz
(3d+2e+f)^w = 3d^2 + 2e^2 + f^2 + 12de + 12df + 6df +4ef

These expressions are solved by:

The square of the first to the last term.
Twice the product of the first and second term.
Twice the product of the first and last term.
Twice the product of the second and last term.

Let's Practice!

See Answers

(r-t+n)^2 = r^2 + t^2 + n^2 + 2rt + 2rn - 2tn
(e+2a+q)^2 = e^2 + 4a^2 + e^2 + 4ae + 2eq + 4q
(m+a-y)(m+a-y)= m^2 + a^2 + y^2 + 2ma -2my - 2ay
(2s + o + 4n) = 4s^2 + O^2 + 16n^2 + 4so - 16sn - 8sn
(2i^2+3a-5n) = 4i^4 + 9a^2 + 25n^2 + 12(i^2)a - 10i(^2)n - 30an
(15a - 4n - 6)^2 = 225a^2 - 16n^2 + 36 - 120an - 48n - 180a
(4a + 4b + 4c)^2 = 16a^2 + 16b^2 + 16c^2 + 24ab + 24ac + 24bc
(9a^2 + 4b^2 – 3c^2)^2 = 81a^4 +16b^4 +9c^4 +72(a^2)b^2 – 54(a^2)c^2- 24(a^2)c^2

07.01.15

Sum and Difference of two terms.

- Can be applied if we are multiplying the difference of squares.

(x + y)(x - y). They can be solved by:

Distributive method:
x^2 - xy + xy - y^2

All patterns always lead to (x^2 - y^2)

Example:

(x+2)(x-2)

(x^2 - 4)

Tip:
The difference of squares doesn't always have to be in order. (x+y)(x-y) -> (x-y)(x+y)
Example:

(x-6)(x+6)

(x^2 - 36)

Example:

(5x-9)(5x+9)

(25x^2 - 81)

Remember that the middle term always lead to zero.

More Examples
(2x-3)(3+2x)

Swap (3+2x) into (2x+3)

(4x^2 - 9)

(2x+3)(3x+2)

(6x^2 + 4x - 9x - 6)

(6x^2 - 5x - 6)

Notice that the example doesn't fit the pattern. So this is just solving for binomials only.

(7/8c + d)(7/8c - d)

(49/64c^2 - d^2)

(x-y)(x+y)(x^2 + y^2)

Use the binary operation:

(x-y)(x+y)
(x^2 - y^2)
(x^2 - y^2)(x^2 + y^2)

Use the general pattern

(x^4 - y^4)

(5y^3 - 8)(5y^3 + 8)(25y^6 + 8)
Use the binary operation:
(5y^3 - 8)(5y^3 + 8)
(25y^6 - 8) (25y^6 + 8)
Use the general pattern
(x^2 - y^2)(x^2 + y^2)
(625y^2 - 4096)

Activity:

Description: This activity will help us model the difference of squares.

Directions:

Prepare a square paper of any size.
label one side as x and y on the other.

If you examine each area, you have formed three dimensions with two areas one one side and one on the other. You can get the area by multiplying the length and width of the area and form this formula: (x+y)(x-y)=(x^2 - y^2).
Let's Practice!

(w – 6)(w + 6)

w^2 - 36

(a + 4c)(a – 4c)

a^2 - 16c^2

(4y – 5d)(4y + 5d)

16y^2 - 25d^2

(3sd + 4f)(4f – 3sd)

9s^2d^2 - 16f^2

(12x – 3)(12x + 3)

144x^2 - 9

(3s^2r^2 + 7q)(3s^2r^2 – 7q)

9s^2r^2 - 49q^2

(lo^4v^5 – 6e^3)(l^3o^4v5 + 6e3)

(l^10 o^8 v^10 - 36e^6)

(5/6g^2a^2 – 2/3d^2)( 5/6g^2a^2 + 2/3d^2)

2/5 3/6g4a4 – 49 d^4

(2sn^qm + 3d^3k) (2sn^qm – 3d^3k)

4s2nq2m – 9d6k

[(s + 2)– 4][(s + 2) + 4]

s2 + 4s – 12

Activity 7: Cubra Cube

A Cubra Cube is a set of cubes and prisms connected by nylon.The task is to represent one to help you understand binomial cubes.

Remember

Volume of a cube = s^3

Rectangular volum = LWH

You can represent a large cube and multiple small cubes.
For each cube, you can see that it has 27 prisms.
Each cube can contain three to six prisms.
The total volume of each cube is 64 cubic inches.
If you mark the large cube with 'a' and the smaller cubes 'b' then combine them you would have a volume of cubic 216 inches.
The new cube formed can have a new volume of 1728 in.
The dimensions formed can be 27 < 216 < 1728

A cubed binomial is equal to the cube of the first term, plus three times the square of the first term by the second term, plus three times the first term by the square of the second term, plus the cube of the second term. Then the cube of the last term. 07.22.15

Activity 8: IRF worksheet

The IRF worksheet will determine your prior knowledge of the topical questions: Revised answer

What makes a Special Product special?

When you think of products, you usually think of it as a result in multiplying numbers. But there are other kinds of products too. One of which is the special product. Special products are commonly found on polynomial algebraic expressions. Special products contain different patterns in order to solve them. examples of special products involved are perfect square trinomials, binomial and trinomial cubes, differencce of terms and many more. So, what makes a product special? Special products contain there different varied patterns, different answers and methods which help you find the answer. Using patterns to simplify mathematical expressions has advantage depending on what the expressions have. Varied methods in special products will help you solve unknown quantities in geometric problems.

What patterns are involved in solving special products?

There are patterns everywhere, our environment, puzzles, computers and mathematical expressions. Note that patterns in special products are uniquely difference.

Perfect square trinomials:

(x+1)^2
        First Term: x^2
        Second Term:2x
        Third Term: 1
        Total Term: x^2 + 2x + 1

    (x+2)^2
        First Term: x^2
        Second Term:4x
        Third Term: 4
    (x+3)^2
        First Term: x^2
        Second Term:6x
        Third Term: 9

    (x+y)^2
        First Term: x^2
        Second Term:2xy
        Third Term: y^2

The first term in the product is squared unlike the first given term.
The last term in the product is also squared unlike the last given term.

Binomial square

A cubed binomial is equal to the cube of the first term, plus three times the square of the first term by the second term, plus three times the first term by the square of the second term, plus the cube of the second term. Then the cube of the last term.

Difference of term:

- Can be applied if we are multiplying the difference of squares.

(x + y)(x - y).

Trinomial Squares:

The square of the first to the last term.
Twice the product of the first and second term.
Twice the product of the first and last term.
Twice the product of the second and last term.

Activity 9: 321 chart!

Three things I found out:

Special Products contain different unique patterns.
Special Products contain different unique methods.
No two special products are the same

Two interesting things:

Special products are very common in algebraic expressions.
Special products have there own rules

One question I still have:

How can distributive property become a universal in special products?

Activity 10: What's the way? That's the way.

Procedure: Write the rules and patterns for Special products.

Perfect square trinomials:

(x+1)^2
        First Term: x^2
        Second Term:2x
        Third Term: 1
        Total Term: x^2 + 2x + 1

    (x+2)^2
        First Term: x^2
        Second Term:4x
        Third Term: 4
    (x+3)^2
        First Term: x^2
        Second Term:6x
        Third Term: 9

    (x+y)^2
        First Term: x^2
        Second Term:2xy
        Third Term: y^2

The first term in the product is squared unlike the first given term.
The last term in the product is also squared unlike the last given term.

Binomial square

A cubed binomial is equal to the cube of the first term, plus three times the square of the first term by the second term, plus three times the first term by the square of the second term, plus the cube of the second term. Then the cube of the last term.

Difference of term:

- Can be applied if we are multiplying the difference of squares.

(x + y)(x - y).

Trinomial Squares:

The square of the first to the last term.
Twice the product of the first and second term.
Twice the product of the first and last term.
Twice the product of the second and last term.

07.29.15

Activity 11: DECISION, DECISION, DECISION!

Directions: Help each person decide what to do by applying your knowledge on special products on each situation.

Jem Boy wants to make his 8-meter square pool into a rectangular one by increasing its length by 2m and decreasing its width by 2m. Jem Boy asked your expertise to help him decide on certain matters.

What will be the new dimensions of Jem Boy's pool?

10m x 6m

What will be the new area of Jem Boy’s pool? What special product will be used?

(8 + 2)(8 – 2)m^2 = (10)(6) = 60m^2; difference of two squares.

If the sides of the square pool is unknown, how will you represent its area?

(x + 2)(x – 2)m^2

If Jem Boy does not want the area of his pool to decrease, will he pursue his plan? Explain your answer.

No, the area will be decreased by 4m^.

Emmanuel wants to tile his rectangular
floor. He has two kinds of tiles to choose from, one of which is larger than the other.

What area will be covered by the 8” x 8” tile? 16” x 16” tile?

64in^2 x 256 in^2

If the rectangular floor has dimensions of 74 x 128,
how many small square tiles are needed to cover it?

(74)(128) = 9472 ÷ 64 = 148 tiles

How many square big tiles are needed to cover the rectangular floor?

If each small tile costs Php 15.00 and each big tiles costs Php 60.00, which tile should Emmanuel use to economize in tiling his floor? Explain why.

Either, because he will spend the same amount whichever tile he will use.

08/05/2015

Activity 13: Beauty in Tile

Description: See different tile patterns on the o flooring of a building and calculate the area.

What is the area represented by the large squares, small squares and rectangles.

Large squares: X^2
Small squares: Y^2
Rectangles: 2xy

What is the total area bounded by each region?

(x^2 + 2xy + y^2)

x^2 + 2xy + y^2

What special product is involved in the problem?

Binomial squaring

What is the area represented by the large squares, small squares.

Large squares: X^2
Small squares: Y^2

What is the sum of all areas in the squares:

9y^2 (x^2 – 9y^2)

(x^2 – 9y^2)

08.12.15

Activity 14: Where's the pattern?

Directions: Take a picture or a sketch that makes use of special products.

Questions:

Did you find any difficulty in looking for patterns where the concept of special products are applied?

No, because patterns that involve special products can be found in the environment.

What are the special products applied?

Perfect Square trinomial: (x^2 + 2xy + y^2)

What did you realize in this activity?

I realized this is not about finding a fixed answer but finding your own.

Activity 15: Let's Debate

Description: Form a team with four or less members and debate about the questions below:

Distributive or Pattern? Which is more effective in solving special products?

Distributive[D]:

If you apply distributive property, you will see that you will get an accurate answer. Distributive property gives you a sure answer whether you check it or not. Distributive property involves long multiplication where most special patterns need to be checking with. Distributive property has one straight-forward rule so no one gets confused and that is to multiply all given numbers and variables to reach the answer. So, this concludes that straight forward rules like distributive property is more efficient, accurate and less confusing.

Patterns[P]:

Straight forward rules like distributive property is more efficient, accurate and less confusing. But applying patterns with their special rules also results more efficient and accurate answers without consuming much time. Patterns are more effective because what's the point in going a very long and hard way, taking much time and effort if it only results the same answer if you use patterns which act like shortcuts? I don't mean cheating or stuff because it's bad. Using patterns are much more recommended when your in a final exam or your in a rush. Patterns are like a quick way to solve something without breaking any rules.

Distributive[D]: Well using patterns may be a great idea but how about checking the answers? Patterns usually drift to Distributive property check their answers so what's the point in taking shortcuts if you will just go back to the beginning of my "long way"?

Which is more effective in life? "Shortcuts" or the "Long Way"?

Activity 16: IRF Worksheet

What makes a Special Product special?

Special Products are "special" because they are very common, and they're worth knowing. Algebraic expressions have their own unique patterns to help us identify how products are answered and why they are answered this way. Heard that before, so what makes a special product "special" exactly? When you think of products, you usually think of it as a result in multiplying numbers. But there are other kinds of products too. One of which is the special product. Special products are commonly found on polynomial algebraic expressions. Special products contain different patterns in order to solve them. examples of special products involved are perfect square trinomials, binomial and trinomial cubes, differencce of terms and many more. So, what makes a product special? Special products contain there different varied patterns, different answers and methods which help you find the answer. Using patterns to simplify mathematical expressions has advantage depending on what the expressions have. Varied methods in special products will help you solve unknown quantities in geometric problems.

08.22.15

Activity 17: Make a Wish

Description: The concept of squaring binomials is used in the field of Genetics through Punnet squares. Punnet squares are used in genetics to model possible gene combinations of off-spring. This Punnet square will help you understand the use of binomial squares.

Direction: Investigate binomial squares using punnet squares and answer the questions.

Example: One cat contains long hair traits and mates with another cat of the same trait. Determine the possibility of having a short haired off-spring.

S s

SS	Ss
Ss	ss

Questions:

What are the chances of having a long haired off-spring than a long one.

Short Hair off-spring: Less
Long Hair off-spring: More

What are the percentage of having off-springs with different genes?

Long hair: 80%
Medium hair: 15%
Short hair: 5%

How many long and short haired off-springs will the mates have?

3-4 Long haired traits
1-0 Short haired traits

How is the concept of Binomial squaring is used in the process?

Binomial squaring involves combining two pairs of things or numbers together similar to genetics combining genes.
Example:

Binomial squares: (X² + 2xy + Y²)
Genetics: (S²+ 2Ss + s²)

Do you think it's possible for the field of genetics to use binomial squaring?

Yes, because binomial squaring is similar to genetics by combining things together to determine particular Genotypes.

Factoring

The figure below is made of 36 tiles. Rearrange them into a rectangle with the same area as the original square. Will you consider changing dimensions? What are the involved concepts?

This module will help you break an expression into different factors and answer topical questions like: "What algebraic expressions involved in solving/factoring geometric expressions?

Activity 1: Like/Unlike

Description: This activity will help gauge how ready you are for this lesson through your responses.
Directions: Answer all questions by writing like or unlike to the table. Like means that you are knowledgeable about the topic and Unlike means you know nothing or little about the topic.

Skills Acquired	Response
Factoring expressions easily	Unlike
Divide polynomials	Unlike
Apply quotient rule of exponents	Unlike
Add and subtract polynomials.	Like
Multiply polynomials	Unlike
Work with special products	Like

Activity 2: IRF Worksheets

Description: Complete the table by answering the initial column of the chart by factoring the expression.

Factors	Initial Answer
4x²–12x	2x(4x-6)
9m²–16	(3m-4)(3m-4)
4a²+12a+9	(2a + 3)²
2x² + 9x*5	x(2x + 45)
2x³ – 8y³	2(x²–4y³)

09.06.15

Activity 3: Message from the king

Definition: Decode the messages associated with the factors

(x-3)(x^2 + 3x + 9)

x-27

3xy^2 (x^2 + 3x + 9)

6x^2 + 3xy^3 - 3xy^2

(x+y)(x-y)

x^2 - xy + xy - y^2

(a+b)(a-b)

a^2 - ab + ab - b^2

(x-5y)(x-5y)

x^2 - 5xy - 5xy - 25y^2

(2x+3)^2

4x + 6x + 6x + 9

Factoring Common Monomial Factors
The process of finding factors of expressions is called factoring. There are many types of factoring, but the first one you will encounter is finding the common monomial factor.

Activity 4: What is Common?

Imagine 3 pictures each showing different people eating in different places in different restaurants.
You can see that the common thing they did is eating
The things that make them different is the place that they're eating at.
The previous activity gave you an idea about finding the Greatest Common Monomial factor works. It appears on every polynomial terms:

Example:

Factor 12x^3y^5 - 20x^5y^2z
Find the GCF of the coefficients

Coefficient of 12 and 20 is 4

Find the common variable with the least exponent.

x and y are both common in the terms and the least expression is x^3 and y^2, thus x^3y^2 is the variable of the GCF.

Divide the polynomial by the GCF

12x^3y^5 - 20x^5y^2z / 4x^3y^2

4x^3y^2(3y^3 - 5x^2z)

Complete the table to practice factoring

POLYNOMIAL	CMF	CMF and QUOTIENT	FACTOR
6m+8	2	3m+4	2(3m+4)
12x^2	4mo^2	3m+0	4mo^2(3m+0)
4(12)+4(8)	4	(12+8)	2(12+8)

Activity 5: Investigation in the classroom

Definition: This activity will help you understand factoring through the difference of squares.

Number Pattern

11(9)= (10+1)(10-1)= 100-1
5(3)= (4+1)(4-1)= 16-1
(n-5)(n+5) = n-25

The products are obtained by using the difference of squares to multiply the terms and find product patterns.

Activity 6: Investigation in paper folding

Description: The activity will help you visualize the pattern of the difference of squares.

Direction:

Get a square paper and label the sides as a.
Cut – out a small square in any of its corner
and label the side of the small square as b.
Cut the remaining figure in half.
Form a rectangle

The area of the square is (a+b)(c+d)
The area of the cut out is (g+f)(d+e)
The area of the new figure is (a+b+c+d+g+f+d+e)
The dimension of the new figure is (a+b+c+d)*(g+f+d+e)
The pattern used is the difference of squares

Activity 7: Pair mo ko nyan

Definition: Create as many expressions in this activity to develop factoring skills.

81m^4 - 121c = (9m^2 - 11c)(9m^2 - 11c)
20a^4 + 25 = (4a^2+5)(4a^2+5)
4(x+1)(x+2) = 4x^2+12x+8
(2x−3)(x−4)2(x2+1) = 2x^5 - 19x^4 + 58x^3 - 67x^2 + 56x - 48
x^2 + 2xy + y^2
49x^2 + 78x + 4
(n-5)(n+5) = n-25

09.22.15

Activity 8: Road map to factor

Description: Use the map as a guide.

Activity 9: Let's tile it up

Directions: Prepare the following:

4 big squares measuring 4” × 4” represent each square...
8 rectangular tiles measuring 4” × 1” represent each square...
6 small squares measuring is 1” × 1” represent each square...

Form squares using:

1 big square tile, 2 rectangular tiles, and 1 small square.

Area: x^2 + 2xy + y^2

1 big square tile, 4 rectangular tiles, and 4 small squares.

Area: x^2 + 4xy + 4y^2

1 big square tile, 6 rectangular tiles, and 9 small squares.

Area: x^2 + 6xy + 9y^2

4 big square tiles, 4 rectangular tiles, and 1 small square.

Area: 4x^2 + 4xy + y^2

4 big square tiles, 8 rectangular tiles, and 4 small squares.

Area: 4x^2 + 8xy + 4y^2

A perfect square trinomial is the result of squaring a binomial. A perfect square trinomial has first and last terms which are perfect squares and a middle term which is twice the product of the square root of the first and last terms.

Activity 10: Perfect Hunt
Description: Factor different binomials found below:

x^2 + 14x + 49
x^2 + 8x + 16
4x^2 + 16x + 16
16x^2 - 24 + 9
49x^2 + 78x + 4
25x^2 + 30x + 9

Factoring perfect square trinomials

Get the square root of the first and last terms.
List down the square root as sum/difference of two terms as the case
may be.
You can use the following relationships to factor perfect square trinomials:

(First term)^2 + 2(First term)(Last term) + (Last term)2

(First term + Last term)^2

(First term)^2 – 2(First term)(Last term) + (Last term)2

(First term – Last term)^2

Exercises:

(m + 6)^2
(7a – 6)^2
2(3h + 1)^2
(4d – 3)^2
(11c2 + 3)2
5f^2 (2f – 3)^2
(a2 b – 3)^2
(5r + 8)^2
(3n + 5d)^2
(14z + 23)^2

Activity 11: Tile once more

Description: You will arrange the tiles according to the instructions given to form a
polygon and find its dimensions afterwards.
Directions:
Form rectangles using the algebra tiles that you prepared. Use
only tiles that are required in each item below.

1 big square tile, 5 rectangular tile and 6 small square tiles.

x^2 + 5x + 6

1 big square tile, 6 rectangular tiles and 8 small square tiles.

x^2 + 6x + 8

2 big square tiles, 7 rectangular tiles and 5 small square tiles.

2x^2 + 7x + 5

3 big square tiles, 7 rectangular tiles and 4 small square tiles

3x^2 + 7x + 4

4 big square tiles, 7 rectangular tiles and 3 small square tiles.

4x^2 + 7x + 3

Cut – out 4 pieces of 3 in. by 3 in. card board and label each as x2
representing its area.Cut – out 8 pieces of rectangular cardboard with dimensions of 3 in. by 1 in. and label each as x representing its area.
Cut – out another square measuring 1 in. by 1 in. and label each as 1 to represent its area.

If you have noticed there are two trinomials that were formed in the preceding activity, trinomials that contains numerical coefficient greater than 1 in its highest degree and trinomials whose numerical coefficient in its highest degree is exactly 1.

10/2/15

Example:

Factor: v^2 + 4v - 21

Solution:

List all Factors of -21

-3	7
-7	3
-21	1
-1	21

Find all factors of -21 whose sum is 4.
7 + -3 = 4
Hence, the factor is (v-3)(v+7) = v^2 + 4v - 21

Remember: To factor trinomials with a leading of 1:

Factor the constant term.
List all factors of the constant that adds up to the middle term and multiplies to the last term.
Write each factor in the pairs as the last term of the binomial factors.

Activity 12: Factor Bingo Game

(n + 4)(n – 5) = n² – n – 20	(n + 2)(n + 9) = n² + 11n + 18	(n + 8)(n + 9) = n² + 17n + 72	(n + 2)(n + 3) = n² + 5n + 6	(n - 9)(n - 8) = n² - 17n + 72	(n + 1)(n + 8) = n2 + 9n + 8
(n – 8)(n + 4) = 8n² + 32n	(n – 7)(n – 5) = n2 -12n + 35	(n + 6)(n + 4) = n² + 10n + 24	(n – 7)(n + 6) = n² – n – 42	(n – 12)(n+4) = n² - 8n - 48	(n – 8)(n +6) = n2 – 2n – 48

10/14/15

Activity 13: We Have!

Description:This game will help you practice your factoring skills
Direction: Factor the following trinomials, the first to factor the most, wins!

Let's get factoring!

8mt-12at-10mh-15ah

(-15ah + -12at) (-10hm + 8mt)

Group the common factor.

4t(2m-3a)-5h(2m-3a)

Factor out the common monomial factor

(2m-3a)(4t-5h)

Factor the binomial and write the remaining factor as the sum and difference.

What if the coefficient of a trinomial isn’t 1?

Trinomials in the form of Nx²+Nx+N can be factored through inspection.

Example:

· Factor: 2x²+ 9x + 7

o Find the factor of the leading term

§ (2x + )(x + )

o Find the factor of the constant term

§ (2x + 7)(x + 1)

o Use the FOIL method

§ (2x + 7)(x + 1) = 2x²+ 9x + 7

· Factor: 6z²-5z – 6

o Find the factor of the leading term

§ (3z + )(2z - )

o Find the factor of the constant term

§ (3z + 2)(2z - 3)

o Use the FOIL method

§ (3z + 2)(2x - 3) = 6z²-5z–6

Activity 14: Famous 4 words

Directions: Factor the following to decode these frequently used words

§ WITH = 4WT - 2WH + 6IT - 3IH

§ HAVE = HV + AV + HE + AE

§ THIS = 10TI – 8TS – 15HI + 12HS

§ FROM = 88FO + 16RO – 99FM – 18RM

§ SOME = 7S + 35OM + 9SE + 45OE

§ WHAT = 42WA + 45WT + 56HA + 72HT

§ YOUR = 35YU + 24RO + 12OU – 72YR

§ WHEN = 72HE + 16WE + 27HM + 6WH

§ WORD = 26WR – 91OR + 35OD – 10WD

Activity 15:

Description: This activity will help your factoring skills influence others.

§ You can state the different kinds of factoring techniques like:

o Difference of terms

o Factoring Monomials

o Perfect Square Trinomial

o Trinomial Squares

o Trinomial Squares = 1

o Trinomial Squares ≠ 1

§ When there are simple factoring methods, there are also complex factoring methods such as:

o Trinomial Squares ≠ 1

o Trial and Error method

§ Learning a new topic for the first time can be difficult but, if you continue to learn about the topic, you will master it and learn that mistakes and difficulties are a part of learning.

Activity 16: Accuracy on factoring

Description: This activity will test your accuracy in factoring:

§ 2k² – 11k + 12

o (K - ) (2K + )

o (K – 4)(2K - 3)

Activity 17:

Description: To summarize what you have learned, complete the chart with examples of factoring techniques.

Factoring Techniques
Factoring Monomials	Perfect Square Trinomial	Difference of Terms	Trinomials A = 1	Trinomials ≠ 1
a(x+y+n)	X²+2xy+y²	(x+y)(x-y)	x²+Nx+N	Nx²+Nx+N

Activity 18: IRF Revisited

Direction: Complete the IRF Worksheet below

Initial	Revised	Final
(2x+3)(2x-4)
9m² – 16m²
(2x-3)(2x+3)
27x³ – 8y²
a³+125b

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Real Life Application: Factoring Trinomials can be used in measuring land areas or how things work. They are also commonly used in the C programming language.

1.A. Polynomials with common monomial factor (Monomial Factors of Polynomials)

03.29.15

Common Monomial Factor:

Can be factored by dividing the polynomials evenly and find common terms and constants.

Example:

6x^2+3x+1; What is the factor?

3(2x^2+x+1)= Factor!

Monomial Factors of Polynomials PRACTICE:

http://www.ck12.org/assessment/ui/views/test.detail.new.html?51d98c885aa41360e92d5618&isPageView=true&referrer=featured_content&ep=http%3A%2F%2Fwww.ck12.org%2Falgebra%2FMonomial-Factors-of-Polynomials%2F

1.B. Special Product (p.13)

Module 1: Special products and Factors (TEACHING GUIDE)

A. Binomal Square - is expressed by the:

Square of the First terms
Twice the product of the first and second term.
Square of the Last term

B. Binomial Cube - is expressed by:

Finding the cube of each term to get the first and last terms.(x)^3 (y)^3
The second term is 3x the product of the first term and the square of the second term. 3(x)^2(y)
The third term is three times the product of the first term and the square of the second term. 3(x)(y)^2

Example 1: (x+y)^2= x^3 + 3v^2y + 3vy^2 + y^3

Example 1: (x-y)^2= x^3 - 3v^2y - 3vy^2 - y^3

1. factor completely different types of polynomials :

Comprehensive test: Rewrite notes.

May 5, 2015

LESSON 1 SPECIAL PRODUCTS

II.Special Products: These are special algebraic expressions whose products are readily seen. They are "special" because they are very common, and they're worth knowing.

Example:

Binomial Cube Pattern

Example:(x+3)(x+3)

= x^2 + 2(x+3) + 3^2

= x^2+2x+6+9

= x^2+2x+15

Sum and Difference of two terms

Example: (x+9)(x-9)

= x*x+x*[-9]+x*9+9*[-9]

= x^2-~~9x+9x~~-81

= x^2-81

math test

https://docs.google.com/document/d/18x2Bnp8tQf820bNalTP0uTtXiqVerhrjYN6HB8PCyRI/pub

May 13, 2013

Special products

- Everything around us have patterns, from the figures found in our environment to solving mathematical expressions. Without patterns everything will look and become messy. The advantages of

having patterns is that everything will go organized and their functions will flow smoothly. Finding mathematical square and cube expressions have patterns in them, enabling them to function or flow smoothly.

Example: Numerical expressions

97*103= 9991
25^2 =625
99*[99^2]= 970299

- The lesson varies activities which all help to solve the question. "How can unknown geometric problems be solved?"

05.20.15

IRF worksheet:

The IRF worksheet will determine your prior knowledge of the topical questions: Initial answer

What makes a special product special?

Special Products are "special" because they are very common, and they're worth knowing.

What patterns are involved in multiplying algebraic expressions?

Algebraic expressions have their own unique patterns to help us identify how products are answered and why they are answered this way.

Algebraic Patterns: This is a collection of algebraic patterns in various methods.

Crossword polynomial puzzle:

a^2 +6a +9 +9b^2

-81 +6b -12ab

+b^2 +8ab +16a

+b^2 +6a

-16a^2 +2ab

+a^2

May 27, 2015

Further study on Special Products (videos):

http://www.showme.com/sh/?h=KEZrSHg

https://www.youtube.com/watch?v=HNU4LKEs1q8&feature=youtu.be

https://www.youtube.com/watch?v=Mm9Ql87sh6s

https://www.youtube.com/watch?v=avVyPhnRZgQ

https://www.ck12.org/algebra/Special-Products-of-Polynomials/

Then answer Activity 2 p.9 in Learning Module

Finding Special Products of Polynomials

To find the special product, you can use two methods:

the Distributive property and the Perfect Square formula.

The Distributive formula:

Multiply the expression by itself or Distribute all terms to another expression.

Perfect Square Formula:

For any real numbers (x+y)^2 = x^2 + 2ab + y^2

Ex.1

Difference of squares:

Distributive Property

(5x-9)(5x+9)= 25x^2 + 45x - 45x - 81

Answer:

Perfect Square Formula:

25x^2 + 2(5x*9) - 81

Answer:

FOIL Method:

5x*5x + 5x*9 + 5x*-9 + -9*9 = 25x^2 + 45x - 45x - 81

Answer:

Square of a Binomial Pattern: A perfect square binomial is a trinomial that when factored gives you the square of a binomial. For example, the trinomial x^2 + 2xy + y^2 is a perfect square binomial because it factors to (x + y)^2.

Equation: (a+b)^2 = a^2 + 2(ab)+ b^2

Special Products of Polynomials test result

https://fbcdn-sphotos-h-a.akamaihd.net/hphotos-ak-xpt1/v/t35.0-12/11255429_1439260943058337_685636252_o.jpg?oh=2ece76935a16322ad7c767fe6ebf1e5f&oe=5568520E&__gda__=1432835133_d682a3ad4bdae62d9e777679bf297a9d

FIRST QUARTER

I. Patterns and Algebra

Patterns:

Using patterns to simplify mathematical expressions has advantage
depending on what the expressions have. These expressions are an example of a mathematical expressions solved by using patterns:

97 × 103 = 9991

25^2 ;25 × 25 = 625

99^2 * 99;99^3;99 x 99 × 99 = 970299

Cross Number puzzle:

Across:

(a + 3) + (a + 3)

a^2 +6a +9

(b + 4a)^2

-81 + 6b

2a(-8a + 3a)

b^2 +6a

(b-4)(b-4)

-16a^2 + 2ab

-2a(b+3–2a)

4a^2 - 2ab - 6a

(5b^2+7a^2)(-5b^2+7a^2)

49a^4 - 25b^4

(a - 6b)(a + 6b)

a^2 - 36b^2

Down:

(a + 9)(a - 9)

a^2 - 81

(3+a+b)^2

a^2 + 2ab + 6a + b^2 + 6b + 9

(3b–4a)(3b–4a)

9b^2 - 12ab + 16a

(-4a + b)(4a + b)

+b^2

06.10.15

Excercise 3

see:Answer Key for Cross number puzzle (above) and Exercise 3

This activity will enable you to review multiplication of polynomials.

Case I.

(x+5)(x-5)

x^2 - 5x + 5x - 5^2

x^2 - 25

(a-b)(a+b)

a^2 + ab - ab - b^2

a^2 - b^2

(x+y)(x-y)

x^2 - xy + xy - y^2

x^2 + xy - y^2

(x-8)(x+8)

x^2 + 8x - 8x - 8^2

x^2 - 64

(2x+5) (2x-5)

4x^2 - 10x + 10x - 5^2

4x^2 - 25

Case II.

(x+5)^2

x^2 + 2(5x) + 5^2

x^2 + 10x + 25

(a-b)^2

a^2 - 2(ab) - b^2

a^2 - ab - b^2

(x+y)^2

x^2 - 2(xy) - y^2

x^2 - xy - y^2

(x-8)^2

x^2 - 2(8x) - 8^2

x^2 - 16x - 64

(2x+5)^2

4x^2 + 2[2x(5)] + 5^2

4x^2 - 20x + 25

Case III.

(x + 5)^3

x^3 + 15x^2 + 75x + 125

(a–b)^3

a^3 – 3a^2 b+ 3ab^2 – b^3

(x+y)^3

x^3 + 3x^2 y + 3xy^2 + y^3

(x+4)^3

x^3 + 3x^2y 12x^2y + 48x + 64

Case IV.

(x+2y)^2

a^2 + b^2 + c^2 + 2ab + 2ac + 2bc

(a+b+c)^2

x^2 + y^2 + z^2 + 2xy + 2xz + 2yz

(m + 2n – 3f)^2

m^2 + 4n^2 + 9f^2 + 4mn – 6fm – 12fn

The goal in this section is to learn and understand key concepts related

06/17/15

Squaring a Binomial

In squaring a Binomial you have to express it as (x+y)^2 or (x+y)(x+y).

Activity 4: Fold to square

Description: This activity is used to help you understand binomial squaring through the method of paper folding. You can also investigate the patterns you find for each fold.

Materials: An 8x8 paper

Procedure:

Fold your paper from an edge to make a crease.
Fold it again from the upper right edge to make another crease.
Continue the activity to another paper but make it in folds of two inches. Then do the same in another on folds of three inches.
After that you should be able to see the patterns below:

You can see that you have formed 4 regions in each paper, each region has a shape of a square.There are at least 8 dimensions on each square.
The area of each region has a pattern of (x+1).
The sum of the areas are 49x^2 + 14x + 1y^2 + 2y.
If you replace 1 by 'y' the sum would possibly become 1y.

These patterns are used to emphasize the paper folding patterns

(x+1)^2

First Term: x^2
Second Term:2x
Third Term: 1
Total Term: x^2 + 2x + 1

(x+2)^2

First Term: x^2
Second Term:4x
Third Term: 4

(x+3)^2

First Term: x^2
Second Term:6x
Third Term: 9

(x+y)^2

First Term: x^2
Second Term:2xy
Third Term: y^2

The pattern you can find above is the fast pattern in solving the square of a binomial.

The first term in the product is squared unlike the first given term.
The last term in the product is also squared unlike the last given term.

Observe the following examples:

(x – 3)^2 = (x)^2 – 3x – 3x + (3)^2
(x + 5)^2 = (x)^2 + 5x + 5x + (5)^2

Let's Practice!

Square the following binomials using the pattern you have learned.

(s + 4)^2 = s^2 + 8s + 16
(w– 5)^2 = w^2 – 10w + 25
(e – 7)^2 = e^2 – 14e + 49
(2q – 4)^2 = 4q^2 – 16q + 16
(3z + 2k)^2 = 9z^2 + 12zk + 4k^2
(5d – 7d^2^t)^2 = 25d^2 – 70d^3^t + 49d^4t^2
(7q^2 * w^2 – 4w^2)^2 = 49q4w4 – 56q2 w4 + 16w4
(2/3e – 6)^2 = 49e^2 – 8e + 36
(45kj – 6)^2 = 16/25k^2j^2 – 48/5kj + 36
[(x + 3) – 5]^2 = x^2 – 7x + 64

Binomial Squares are one of the many patterns in special products. But there are still many patterns you can solve.

06.24.15

For any real number (x+y+z)^2

(x+y+z)(x+y+z)

x^2 + y^2 + z^2 + 2(x)(y) + 2(x)(z) + 2(y)(z)

x^2 + y^2 + z^2 + 2xy + 2xz + 2yz

Example:

(2x + 8y + 12)^2

2x^2 + 8y^2 + 12^2 + 2(2x)(8y)+ 2(2x)(12) + 2(8y)(12)

4x^2 + 32y^2 + 144 + 32xy + 48xy + 192y

Activity 5: Discover me After!

Objective: Through paper folding and cutting, you will discover a pattern that will help you understand how trinomials are squared.
Directions:

Get a 10x10 square paper.
Mark the vertical side with numbers (Example 7,3,1).
Mark the horizontal side with letters (Example a,b,c).
Fold the numbered side vertically and make a crease.
Do the same thing on the horizontal side.

Descriptions:

As you can see, there are 9 regions formed with a 3x3 dimension. If you represent a region with a letter without replacing the number, you will see that you can represent (7a + 3b + a).

Observe the following:

(x+y+z)^2 = x^2 + y^2 + z^2 + 2xy + 2xz + 2yz
(x+y-z)^2 = x^2 + y^2 + z^2 + 2xy - 2xz - 2yz
(3d+2e+f)^w = 3d^2 + 2e^2 + f^2 + 12de + 12df + 6df +4ef

These expressions are solved by:

The square of the first to the last term.
Twice the product of the first and second term.
Twice the product of the first and last term.
Twice the product of the second and last term.

Let's Practice!

See Answers

(r-t+n)^2 = r^2 + t^2 + n^2 + 2rt + 2rn - 2tn
(e+2a+q)^2 = e^2 + 4a^2 + e^2 + 4ae + 2eq + 4q
(m+a-y)(m+a-y)= m^2 + a^2 + y^2 + 2ma -2my - 2ay
(2s + o + 4n) = 4s^2 + O^2 + 16n^2 + 4so - 16sn - 8sn
(2i^2+3a-5n) = 4i^4 + 9a^2 + 25n^2 + 12(i^2)a - 10i(^2)n - 30an
(15a - 4n - 6)^2 = 225a^2 - 16n^2 + 36 - 120an - 48n - 180a
(4a + 4b + 4c)^2 = 16a^2 + 16b^2 + 16c^2 + 24ab + 24ac + 24bc
(9a^2 + 4b^2 – 3c^2)^2 = 81a^4 +16b^4 +9c^4 +72(a^2)b^2 – 54(a^2)c^2- 24(a^2)c^2

07.01.15

Sum and Difference of two terms.

- Can be applied if we are multiplying the difference of squares.

(x + y)(x - y). They can be solved by:

Distributive method:
x^2 - xy + xy - y^2

All patterns always lead to (x^2 - y^2)

Example:

(x+2)(x-2)

(x^2 - 4)

Tip:
The difference of squares doesn't always have to be in order. (x+y)(x-y) -> (x-y)(x+y)
Example:

(x-6)(x+6)

(x^2 - 36)

Example:

(5x-9)(5x+9)

(25x^2 - 81)

Remember that the middle term always lead to zero.

More Examples
(2x-3)(3+2x)

Swap (3+2x) into (2x+3)

(4x^2 - 9)

(2x+3)(3x+2)

(6x^2 + 4x - 9x - 6)

(6x^2 - 5x - 6)

Notice that the example doesn't fit the pattern. So this is just solving for binomials only.

(7/8c + d)(7/8c - d)

(49/64c^2 - d^2)

(x-y)(x+y)(x^2 + y^2)

Use the binary operation:

(x-y)(x+y)
(x^2 - y^2)
(x^2 - y^2)(x^2 + y^2)

Use the general pattern

(x^4 - y^4)

(5y^3 - 8)(5y^3 + 8)(25y^6 + 8)
Use the binary operation:
(5y^3 - 8)(5y^3 + 8)
(25y^6 - 8) (25y^6 + 8)
Use the general pattern
(x^2 - y^2)(x^2 + y^2)
(625y^2 - 4096)

Activity:

Description: This activity will help us model the difference of squares.

Directions:

Prepare a square paper of any size.
label one side as x and y on the other.

(w – 6)(w + 6)

w^2 - 36

(a + 4c)(a – 4c)

a^2 - 16c^2

(4y – 5d)(4y + 5d)

16y^2 - 25d^2

(3sd + 4f)(4f – 3sd)

9s^2d^2 - 16f^2

(12x – 3)(12x + 3)

144x^2 - 9

(3s^2r^2 + 7q)(3s^2r^2 – 7q)

9s^2r^2 - 49q^2

(lo^4v^5 – 6e^3)(l^3o^4v5 + 6e3)

(l^10 o^8 v^10 - 36e^6)

(5/6g^2a^2 – 2/3d^2)( 5/6g^2a^2 + 2/3d^2)

2/5 3/6g4a4 – 49 d^4

(2sn^qm + 3d^3k) (2sn^qm – 3d^3k)

4s2nq2m – 9d6k

[(s + 2)– 4][(s + 2) + 4]

s2 + 4s – 12

Activity 7: Cubra Cube

A Cubra Cube is a set of cubes and prisms connected by nylon.The task is to represent one to help you understand binomial cubes.

Remember

Volume of a cube = s^3

Rectangular volum = LWH

You can represent a large cube and multiple small cubes.
For each cube, you can see that it has 27 prisms.
Each cube can contain three to six prisms.
The total volume of each cube is 64 cubic inches.
If you mark the large cube with 'a' and the smaller cubes 'b' then combine them you would have a volume of cubic 216 inches.
The new cube formed can have a new volume of 1728 in.
The dimensions formed can be 27 < 216 < 1728

Activity 8: IRF worksheet

The IRF worksheet will determine your prior knowledge of the topical questions: Revised answer

What makes a Special Product special?

When you think of products, you usually think of it as a result in multiplying numbers. But there are other kinds of products too. One of which is the special product. Special products are commonly found on polynomial algebraic expressions. Special products contain different patterns in order to solve them. examples of special products involved are perfect square trinomials, binomial and trinomial cubes, differencce of terms and many more. So, what makes a product special? Special products contain there different varied patterns, different answers and methods which help you find the answer. Using patterns to simplify mathematical expressions has advantage depending on what the expressions have. Varied methods in special products will help you solve unknown quantities in geometric problems.

What patterns are involved in solving special products?

There are patterns everywhere, our environment, puzzles, computers and mathematical expressions. Note that patterns in special products are uniquely difference.

Perfect square trinomials:

(x+1)^2
        First Term: x^2
        Second Term:2x
        Third Term: 1
        Total Term: x^2 + 2x + 1

    (x+2)^2
        First Term: x^2
        Second Term:4x
        Third Term: 4
    (x+3)^2
        First Term: x^2
        Second Term:6x
        Third Term: 9

    (x+y)^2
        First Term: x^2
        Second Term:2xy
        Third Term: y^2

The first term in the product is squared unlike the first given term.
The last term in the product is also squared unlike the last given term.

Binomial square

A cubed binomial is equal to the cube of the first term, plus three times the square of the first term by the second term, plus three times the first term by the square of the second term, plus the cube of the second term. Then the cube of the last term.

Difference of term:

- Can be applied if we are multiplying the difference of squares.

(x + y)(x - y).

Trinomial Squares:

The square of the first to the last term.
Twice the product of the first and second term.
Twice the product of the first and last term.
Twice the product of the second and last term.

Activity 9: 321 chart!

Three things I found out:

Special Products contain different unique patterns.
Special Products contain different unique methods.
No two special products are the same

Two interesting things:

Special products are very common in algebraic expressions.
Special products have there own rules

One question I still have:

How can distributive property become a universal in special products?

Activity 10: What's the way? That's the way.

Procedure: Write the rules and patterns for Special products.

Perfect square trinomials:

(x+1)^2
        First Term: x^2
        Second Term:2x
        Third Term: 1
        Total Term: x^2 + 2x + 1

    (x+2)^2
        First Term: x^2
        Second Term:4x
        Third Term: 4
    (x+3)^2
        First Term: x^2
        Second Term:6x
        Third Term: 9

    (x+y)^2
        First Term: x^2
        Second Term:2xy
        Third Term: y^2

The first term in the product is squared unlike the first given term.
The last term in the product is also squared unlike the last given term.

Binomial square

A cubed binomial is equal to the cube of the first term, plus three times the square of the first term by the second term, plus three times the first term by the square of the second term, plus the cube of the second term. Then the cube of the last term.

Difference of term:

- Can be applied if we are multiplying the difference of squares.

(x + y)(x - y).

Trinomial Squares:

The square of the first to the last term.
Twice the product of the first and second term.
Twice the product of the first and last term.
Twice the product of the second and last term.

07.29.15

Activity 11: DECISION, DECISION, DECISION!

Directions: Help each person decide what to do by applying your knowledge on special products on each situation.

Jem Boy wants to make his 8-meter square pool into a rectangular one by increasing its length by 2m and decreasing its width by 2m. Jem Boy asked your expertise to help him decide on certain matters.

What will be the new dimensions of Jem Boy's pool?

10m x 6m

What will be the new area of Jem Boy’s pool? What special product will be used?

(8 + 2)(8 – 2)m^2 = (10)(6) = 60m^2; difference of two squares.

If the sides of the square pool is unknown, how will you represent its area?

(x + 2)(x – 2)m^2

If Jem Boy does not want the area of his pool to decrease, will he pursue his plan? Explain your answer.

No, the area will be decreased by 4m^.

Emmanuel wants to tile his rectangular
floor. He has two kinds of tiles to choose from, one of which is larger than the other.

What area will be covered by the 8” x 8” tile? 16” x 16” tile?

64in^2 x 256 in^2

If the rectangular floor has dimensions of 74 x 128,
how many small square tiles are needed to cover it?

(74)(128) = 9472 ÷ 64 = 148 tiles

How many square big tiles are needed to cover the rectangular floor?

If each small tile costs Php 15.00 and each big tiles costs Php 60.00, which tile should Emmanuel use to economize in tiling his floor? Explain why.

Either, because he will spend the same amount whichever tile he will use.

08/05/2015

Activity 13: Beauty in Tile

Description: See different tile patterns on the o flooring of a building and calculate the area.

What is the area represented by the large squares, small squares and rectangles.

Large squares: X^2
Small squares: Y^2
Rectangles: 2xy

What is the total area bounded by each region?

(x^2 + 2xy + y^2)

x^2 + 2xy + y^2

What special product is involved in the problem?

Binomial squaring

What is the area represented by the large squares, small squares.

Large squares: X^2
Small squares: Y^2

What is the sum of all areas in the squares:

9y^2 (x^2 – 9y^2)

(x^2 – 9y^2)

08.12.15

Activity 14: Where's the pattern?

Directions: Take a picture or a sketch that makes use of special products.

Questions:

Did you find any difficulty in looking for patterns where the concept of special products are applied?

No, because patterns that involve special products can be found in the environment.

What are the special products applied?

Perfect Square trinomial: (x^2 + 2xy + y^2)

What did you realize in this activity?

I realized this is not about finding a fixed answer but finding your own.

Activity 15: Let's Debate

Description: Form a team with four or less members and debate about the questions below:

Distributive or Pattern? Which is more effective in solving special products?

Distributive[D]:

If you apply distributive property, you will see that you will get an accurate answer. Distributive property gives you a sure answer whether you check it or not. Distributive property involves long multiplication where most special patterns need to be checking with. Distributive property has one straight-forward rule so no one gets confused and that is to multiply all given numbers and variables to reach the answer. So, this concludes that straight forward rules like distributive property is more efficient, accurate and less confusing.

Patterns[P]:

Straight forward rules like distributive property is more efficient, accurate and less confusing. But applying patterns with their special rules also results more efficient and accurate answers without consuming much time. Patterns are more effective because what's the point in going a very long and hard way, taking much time and effort if it only results the same answer if you use patterns which act like shortcuts? I don't mean cheating or stuff because it's bad. Using patterns are much more recommended when your in a final exam or your in a rush. Patterns are like a quick way to solve something without breaking any rules.

Distributive[D]: Well using patterns may be a great idea but how about checking the answers? Patterns usually drift to Distributive property check their answers so what's the point in taking shortcuts if you will just go back to the beginning of my "long way"?

Which is more effective in life? "Shortcuts" or the "Long Way"?

Activity 16: IRF Worksheet

What makes a Special Product special?

Special Products are "special" because they are very common, and they're worth knowing. Algebraic expressions have their own unique patterns to help us identify how products are answered and why they are answered this way. Heard that before, so what makes a special product "special" exactly? When you think of products, you usually think of it as a result in multiplying numbers. But there are other kinds of products too. One of which is the special product. Special products are commonly found on polynomial algebraic expressions. Special products contain different patterns in order to solve them. examples of special products involved are perfect square trinomials, binomial and trinomial cubes, differencce of terms and many more. So, what makes a product special? Special products contain there different varied patterns, different answers and methods which help you find the answer. Using patterns to simplify mathematical expressions has advantage depending on what the expressions have. Varied methods in special products will help you solve unknown quantities in geometric problems.

08.22.15

Activity 17: Make a Wish

Direction: Investigate binomial squares using punnet squares and answer the questions.

Example: One cat contains long hair traits and mates with another cat of the same trait. Determine the possibility of having a short haired off-spring.

S s

SS	Ss
Ss	ss

Questions:

What are the chances of having a long haired off-spring than a long one.

Short Hair off-spring: Less
Long Hair off-spring: More

What are the percentage of having off-springs with different genes?

Long hair: 80%
Medium hair: 15%
Short hair: 5%

How many long and short haired off-springs will the mates have?

3-4 Long haired traits
1-0 Short haired traits

How is the concept of Binomial squaring is used in the process?

Binomial squaring involves combining two pairs of things or numbers together similar to genetics combining genes.
Example:

Binomial squares: (X² + 2xy + Y²)
Genetics: (S²+ 2Ss + s²)

Do you think it's possible for the field of genetics to use binomial squaring?

Yes, because binomial squaring is similar to genetics by combining things together to determine particular Genotypes.

Factoring

The figure below is made of 36 tiles. Rearrange them into a rectangle with the same area as the original square. Will you consider changing dimensions? What are the involved concepts?

This module will help you break an expression into different factors and answer topical questions like: "What algebraic expressions involved in solving/factoring geometric expressions?

Activity 1: Like/Unlike

Skills Acquired	Response
Factoring expressions easily	Unlike
Divide polynomials	Unlike
Apply quotient rule of exponents	Unlike
Add and subtract polynomials.	Like
Multiply polynomials	Unlike
Work with special products	Like

Activity 2: IRF Worksheets

Description: Complete the table by answering the initial column of the chart by factoring the expression.

Factors	Initial Answer
4x²–12x	2x(4x-6)
9m²–16	(3m-4)(3m-4)
4a²+12a+9	(2a + 3)²
2x² + 9x*5	x(2x + 45)
2x³ – 8y³	2(x²–4y³)

09.06.15

Activity 3: Message from the king

Definition: Decode the messages associated with the factors

(x-3)(x^2 + 3x + 9)

x-27

3xy^2 (x^2 + 3x + 9)

6x^2 + 3xy^3 - 3xy^2

(x+y)(x-y)

x^2 - xy + xy - y^2

(a+b)(a-b)

a^2 - ab + ab - b^2

(x-5y)(x-5y)

x^2 - 5xy - 5xy - 25y^2

(2x+3)^2

4x + 6x + 6x + 9

Factor 12x^3y^5 - 20x^5y^2z
Find the GCF of the coefficients

Coefficient of 12 and 20 is 4

Find the common variable with the least exponent.

x and y are both common in the terms and the least expression is x^3 and y^2, thus x^3y^2 is the variable of the GCF.

Divide the polynomial by the GCF

12x^3y^5 - 20x^5y^2z / 4x^3y^2

4x^3y^2(3y^3 - 5x^2z)

Complete the table to practice factoring

POLYNOMIAL	CMF	CMF and QUOTIENT	FACTOR
6m+8	2	3m+4	2(3m+4)
12x^2	4mo^2	3m+0	4mo^2(3m+0)
4(12)+4(8)	4	(12+8)	2(12+8)

Activity 5: Investigation in the classroom

Definition: This activity will help you understand factoring through the difference of squares.

Number Pattern

11(9)= (10+1)(10-1)= 100-1
5(3)= (4+1)(4-1)= 16-1
(n-5)(n+5) = n-25

Get a square paper and label the sides as a.
Cut – out a small square in any of its corner
and label the side of the small square as b.
Cut the remaining figure in half.
Form a rectangle

81m^4 - 121c = (9m^2 - 11c)(9m^2 - 11c)
20a^4 + 25 = (4a^2+5)(4a^2+5)
4(x+1)(x+2) = 4x^2+12x+8
(2x−3)(x−4)2(x2+1) = 2x^5 - 19x^4 + 58x^3 - 67x^2 + 56x - 48
x^2 + 2xy + y^2
49x^2 + 78x + 4
(n-5)(n+5) = n-25

09.22.15

Activity 8: Road map to factor

Description: Use the map as a guide.

Activity 9: Let's tile it up

Directions: Prepare the following:

4 big squares measuring 4” × 4” represent each square...
8 rectangular tiles measuring 4” × 1” represent each square...
6 small squares measuring is 1” × 1” represent each square...

Form squares using:

1 big square tile, 2 rectangular tiles, and 1 small square.

Area: x^2 + 2xy + y^2

1 big square tile, 4 rectangular tiles, and 4 small squares.

Area: x^2 + 4xy + 4y^2

1 big square tile, 6 rectangular tiles, and 9 small squares.

Area: x^2 + 6xy + 9y^2

4 big square tiles, 4 rectangular tiles, and 1 small square.

Area: 4x^2 + 4xy + y^2

4 big square tiles, 8 rectangular tiles, and 4 small squares.

Area: 4x^2 + 8xy + 4y^2

x^2 + 14x + 49
x^2 + 8x + 16
4x^2 + 16x + 16
16x^2 - 24 + 9
49x^2 + 78x + 4
25x^2 + 30x + 9

(First term)^2 + 2(First term)(Last term) + (Last term)2

(First term + Last term)^2

(First term)^2 – 2(First term)(Last term) + (Last term)2

(First term – Last term)^2

Exercises:

(m + 6)^2
(7a – 6)^2
2(3h + 1)^2
(4d – 3)^2
(11c2 + 3)2
5f^2 (2f – 3)^2
(a2 b – 3)^2
(5r + 8)^2
(3n + 5d)^2
(14z + 23)^2

1 big square tile, 5 rectangular tile and 6 small square tiles.

x^2 + 5x + 6

1 big square tile, 6 rectangular tiles and 8 small square tiles.

x^2 + 6x + 8

2 big square tiles, 7 rectangular tiles and 5 small square tiles.

2x^2 + 7x + 5

3 big square tiles, 7 rectangular tiles and 4 small square tiles

3x^2 + 7x + 4

4 big square tiles, 7 rectangular tiles and 3 small square tiles.

4x^2 + 7x + 3

Cut – out 4 pieces of 3 in. by 3 in. card board and label each as x2
representing its area.Cut – out 8 pieces of rectangular cardboard with dimensions of 3 in. by 1 in. and label each as x representing its area.
Cut – out another square measuring 1 in. by 1 in. and label each as 1 to represent its area.

Factor: v^2 + 4v - 21

Solution:

List all Factors of -21

-3	7
-7	3
-21	1
-1	21

Find all factors of -21 whose sum is 4.
7 + -3 = 4
Hence, the factor is (v-3)(v+7) = v^2 + 4v - 21

Remember: To factor trinomials with a leading of 1:

Factor the constant term.
List all factors of the constant that adds up to the middle term and multiplies to the last term.
Write each factor in the pairs as the last term of the binomial factors.

Activity 12: Factor Bingo Game

(n + 4)(n – 5) = n² – n – 20	(n + 2)(n + 9) = n² + 11n + 18	(n + 8)(n + 9) = n² + 17n + 72	(n + 2)(n + 3) = n² + 5n + 6	(n - 9)(n - 8) = n² - 17n + 72	(n + 1)(n + 8) = n2 + 9n + 8
(n – 8)(n + 4) = 8n² + 32n	(n – 7)(n – 5) = n2 -12n + 35	(n + 6)(n + 4) = n² + 10n + 24	(n – 7)(n + 6) = n² – n – 42	(n – 12)(n+4) = n² - 8n - 48	(n – 8)(n +6) = n2 – 2n – 48

10/14/15

Activity 13: We Have!

Description:This game will help you practice your factoring skills
Direction: Factor the following trinomials, the first to factor the most, wins!

Let's get factoring!

8mt-12at-10mh-15ah

(-15ah + -12at) (-10hm + 8mt)

Group the common factor.

4t(2m-3a)-5h(2m-3a)

Factor out the common monomial factor

(2m-3a)(4t-5h)

Factor the binomial and write the remaining factor as the sum and difference.

What if the coefficient of a trinomial isn’t 1?

Trinomials in the form of Nx²+Nx+N can be factored through inspection.

Example:

· Factor: 2x²+ 9x + 7

o Find the factor of the leading term

§ (2x + )(x + )

o Find the factor of the constant term

§ (2x + 7)(x + 1)

o Use the FOIL method

§ (2x + 7)(x + 1) = 2x²+ 9x + 7

· Factor: 6z²-5z – 6

o Find the factor of the leading term

§ (3z + )(2z - )

o Find the factor of the constant term

§ (3z + 2)(2z - 3)

o Use the FOIL method

§ (3z + 2)(2x - 3) = 6z²-5z–6

Activity 14: Famous 4 words

Directions: Factor the following to decode these frequently used words

§ WITH = 4WT - 2WH + 6IT - 3IH

§ HAVE = HV + AV + HE + AE

§ THIS = 10TI – 8TS – 15HI + 12HS

§ FROM = 88FO + 16RO – 99FM – 18RM

§ SOME = 7S + 35OM + 9SE + 45OE

§ WHAT = 42WA + 45WT + 56HA + 72HT

§ YOUR = 35YU + 24RO + 12OU – 72YR

§ WHEN = 72HE + 16WE + 27HM + 6WH

§ WORD = 26WR – 91OR + 35OD – 10WD

Activity 15:

Description: This activity will help your factoring skills influence others.

§ You can state the different kinds of factoring techniques like:

o Difference of terms

o Factoring Monomials

o Perfect Square Trinomial

o Trinomial Squares

o Trinomial Squares = 1

o Trinomial Squares ≠ 1

§ When there are simple factoring methods, there are also complex factoring methods such as:

o Trinomial Squares ≠ 1

o Trial and Error method

§ Learning a new topic for the first time can be difficult but, if you continue to learn about the topic, you will master it and learn that mistakes and difficulties are a part of learning.

Activity 16: Accuracy on factoring

Description: This activity will test your accuracy in factoring:

§ 2k² – 11k + 12

o (K - ) (2K + )

o (K – 4)(2K - 3)

Activity 17:

Description: To summarize what you have learned, complete the chart with examples of factoring techniques.

Factoring Techniques
Factoring Monomials	Perfect Square Trinomial	Difference of Terms	Trinomials A = 1	Trinomials ≠ 1
a(x+y+n)	X²+2xy+y²	(x+y)(x-y)	x²+Nx+N	Nx²+Nx+N

Activity 18: IRF Revisited

Direction: Complete the IRF Worksheet below

Initial	Revised	Final
(2x+3)(2x-4)
9m² – 16m²
(2x-3)(2x+3)
27x³ – 8y²
a³+125b

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Real Life Application: Factoring Trinomials can be used in measuring land areas or how things work. They are also commonly used in the C programming language.

10/28/15
Activity 19: Spotting errors
Description: This activity will check how well you apply your factoring skills.
Direction: Spot the errors on the factoring problems below:

Is x2-4x-12 = 12-4x-x2?

x2-4x-12 = 12-4x-x2
x2-4x-12 = (x+2)(x+6)
12-4x-x2 = (x-6)(x+2)

Apply the difference of terms in 3x2-12x

Answer: 3x2-12x = 3x(x2-4) = (x-2)(x+2)

Is x2+36 factorable by difference of squares?

Answer: No, because x2-36 has missing parts, or may have been a result of another factor.

Make a generalization for errors found below:

x2+4 = Not factorable
2.6x2-9 = Not factorable
4x2y5 - 12x3y6 + 2y2 = Not factorable

Conclusion: All polynomials above cannot be factored.

Activity 20: IRF Revisited

Initial Revised Final

Initial		Revised		Final
		(2x+3)(2x-4)		(2x+3)(2x-4)
	9m² – 16m²		9m² – 16m²		(3m-4n)(4m+4n)
			(2x-3)(2x+3)		(2x-3)(2x+3)
	27x³ – 8y²		27x³ – 8y²		27x³ – 8y²
	a³+125b		a³+125b		(a+5b)(a²-5b+25b²)

Activity 21: 2=1 is possible to me!
How can 2=1 be possible?
Answer:

a2=b2

a2-b2 = b(a-b)

(b)(b) = 2b

2b/b = 1

2 = 1!

Activity 22: Journal writing

Description: Reflect your lesson by completing the sentences

· I learned that… Factoring is putting special products into question form.
· I’m surprised that… Factoring is the reversed of special products
· I noticed that… Factoring had many methods to be solved.
· I discovered that… All factoring methods lead back to the basic method of factoring.

1.A. Polynomials with common monomial factor (Monomial Factors of Polynomials)

03.29.15

Common Monomial Factor:

Can be factored by dividing the polynomials evenly and find common terms and constants.

Example:

6x^2+3x+1; What is the factor?

3(2x^2+x+1)= Factor!

Monomial Factors of Polynomials PRACTICE:

1.B. Special Product (p.13)

Module 1: Special products and Factors (TEACHING GUIDE)

A. Binomal Square - is expressed by the:

Square of the First terms
Twice the product of the first and second term.
Square of the Last term

B. Binomial Cube - is expressed by:

Finding the cube of each term to get the first and last terms.(x)^3 (y)^3
The second term is 3x the product of the first term and the square of the second term. 3(x)^2(y)
The third term is three times the product of the first term and the square of the second term. 3(x)(y)^2

Example 1: (x+y)^2= x^3 + 3v^2y + 3vy^2 + y^3

Example 1: (x-y)^2= x^3 - 3v^2y - 3vy^2 - y^3

1. factor completely different types of polynomials :

Comprehensive test: Rewrite notes.

May 5, 2015

LESSON 1 SPECIAL PRODUCTS

II.Special Products: These are special algebraic expressions whose products are readily seen. They are "special" because they are very common, and they're worth knowing.

Example:

Binomial Cube Pattern

Example:(x+3)(x+3)

= x^2 + 2(x+3) + 3^2

= x^2+2x+6+9

= x^2+2x+15

Sum and Difference of two terms

Example: (x+9)(x-9)

= x*x+x*[-9]+x*9+9*[-9]

= x^2-~~9x+9x~~-81

= x^2-81

math test

https://docs.google.com/document/d/18x2Bnp8tQf820bNalTP0uTtXiqVerhrjYN6HB8PCyRI/pub

May 13, 2013

Special products

- Everything around us have patterns, from the figures found in our environment to solving mathematical expressions. Without patterns everything will look and become messy. The advantages of

Example: Numerical expressions

97*103= 9991
25^2 =625
99*[99^2]= 970299

- The lesson varies activities which all help to solve the question. "How can unknown geometric problems be solved?"

05.20.15

IRF worksheet:

The IRF worksheet will determine your prior knowledge of the topical questions: Initial answer

What makes a special product special?

Special Products are "special" because they are very common, and they're worth knowing.

What patterns are involved in multiplying algebraic expressions?

Algebraic expressions have their own unique patterns to help us identify how products are answered and why they are answered this way.

Algebraic Patterns: This is a collection of algebraic patterns in various methods.

Crossword polynomial puzzle:

a^2 +6a +9 +9b^2

-81 +6b -12ab

+b^2 +8ab +16a

+b^2 +6a

-16a^2 +2ab

+a^2

May 27, 2015

Further study on Special Products (videos):

http://www.showme.com/sh/?h=KEZrSHg

https://www.youtube.com/watch?v=HNU4LKEs1q8&feature=youtu.be

https://www.youtube.com/watch?v=Mm9Ql87sh6s

https://www.youtube.com/watch?v=avVyPhnRZgQ

https://www.ck12.org/algebra/Special-Products-of-Polynomials/

Then answer Activity 2 p.9 in Learning Module

Finding Special Products of Polynomials

To find the special product, you can use two methods:

the Distributive property and the Perfect Square formula.

The Distributive formula:

Multiply the expression by itself or Distribute all terms to another expression.

Perfect Square Formula:

For any real numbers (x+y)^2 = x^2 + 2ab + y^2

Ex.1

Difference of squares:

Distributive Property

(5x-9)(5x+9)= 25x^2 + 45x - 45x - 81

Answer:

Perfect Square Formula:

25x^2 + 2(5x*9) - 81

Answer:

FOIL Method:

5x*5x + 5x*9 + 5x*-9 + -9*9 = 25x^2 + 45x - 45x - 81

Answer:

Equation: (a+b)^2 = a^2 + 2(ab)+ b^2

Special Products of Polynomials test result

Xander Home Study Guide

Home Study Guide

K to 12 Grade 8 MATH

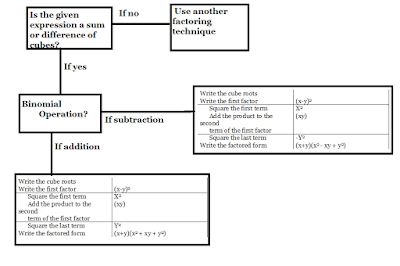
No comments:

Post a Comment

Blog Archive

Translate